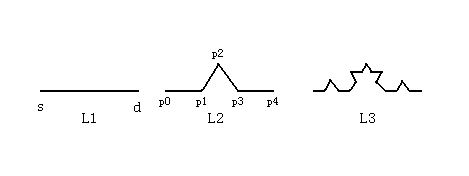
Koch Curve is very common in fractal. It has infinite length. The figure above illustrates the creation of a Koch Curve. A line segment L1 (a->d) is given. It is cut into three equal parts. L2 is obtained by rotating the middle part counter-clockwise to vector s->d. The length satisfies the constraint p0p1 = p1p2 = p2p3 = p3p4. We further process on p0->p1, p1->p2, p2->p3, p3->p4 to obtain L3. We proceed with such iteration to obtain Koch Curve. Since the length is increased by 4/3 each iteration, the length of Koch Curve is infinite. With given s and d, you are to provide the result of the n-th iteration.

There are multiple tests, in each test.

The first line contains an integer n (1 <= n <= 7).

The second line contains four floating numbers sx, sy, dx, dy.

For each test print the vertex in the order from s to d. Keep two digits after decimal point.

Print a blank line after each case.