A binary image, such as the one shown in Figure 2(a), is usually represented as an array of binary entries, i.e., each entry of the array has value 0 or 1. Figure 2(b) shows the array that represents the binary image in Figure 2(a). To store the binary image of Figure 2(b), the so-called quad tree partition is usually used. For an N x N array, N <= 512 and N = 2^i for some positive integer i, if the entries do not have the same value, then it is partitioned into four N/2 x N/2 arrays, as shown in Figure 2(c). If an N/2 x N/2 array does not have the same binary value, such as the upper right and lower right N/2 x N/2 arrays in Figure 2(c), then we can divide it into four N/4 x N/4 arrays again. These N/4 x N/4 arrays in turn can also, if needed, be divided into four N/8 x N/8 arrays, etc.. The quad tree partition is completed when the whole array is partitioned into arrays of various size in which each array contains only one binary value. Figure 2(c) contains the arrays after the quad tree partition is completed.

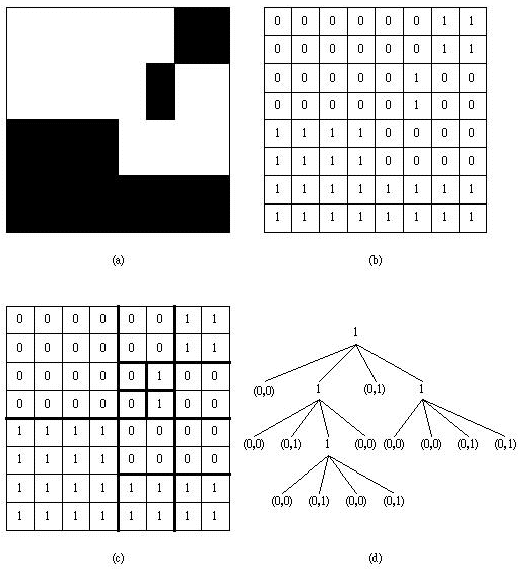
Figure 2: A binary image (a), its array representation (b), its quad tree partition (c), and its quad tree representation (d).
Instead of storing the binary image of Figure 2(a), we only need to store the quad tree in the form as Figure 2(d) which is encoded from Figure 2(c). In Figure 2(d), each node represents an array of Figure 2(c) in which the root node represents the original array. If the value of a node in the tree is 1, then it means that its corresponding array needs to be decomposed into four smaller arrays. Otherwise, a node will have a pair of values and the first one is 0. It means that its corresponding array is not necessary to decompose any more. In this case, the second value is 0 (respectively, 1) to indicate that all the entries in the array are 0 (respectively, 1). Thus, we only need to store the tree of Figure 2(d) to replace storing the binary image of Figure 2(a). The way to store the tree of Figure 2(d) can be represented by the following code:
(1)(0,0)(1)(0,1)(1)(0,0)(0,1)(1)(0,0)(0,0)(0,0)(0,1)(0,1)(0,0)(0,1)(0,0)(0,1).
This code is just to list the values of the nodes from the root to leaves and from left to right in each level. Deleting the parentheses and commas, we can obtain a binary number 100101100011000000010100010001 which is equal to 258C0511 in hexadecimal. You are asked to design a program for finding the resulting hexadecimal value for each given image.

There is an integer number k, 1 <= k <= 100, in the first line to indicate the number of test cases. In each test case, the first line is also a positive integer N indicating that the binary image is an N x N array, where N <= 512 and N = 2^i for some positive integer i. Then, an N x N binary array is followed in which at least one blank is between any two elements.

The bit stream (in hexadecimal) used to code each input array.