给定2 个m*n方格阵列组成的图形A和B，每个方格的颜色为黑色或白色。行列变换问题的每一步变换可以交换任意2 行或2 列方格的颜色，或者将某行或某列颠倒。上述每次变换算作一步。试设计一个算法，计算最少需要多少步，才能将图形A变换为图形B。

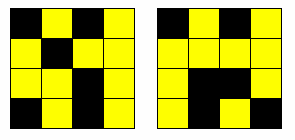
     图形A                                            图形B
图6-8 行列变换问题

对于给定的2 个方格阵列，计算将图形A变换为图形B的最少变换次数。

输入数据的第1 行有2 个正整数m和n。以下的m行是方格阵列的初始状态A，每行有n 个数字表示该行方格的状态，0 表示白色，1 表示黑色。接
着的m行是方格阵列的目标状态B。

将计算出的最少变换次数和相应的变换序列输出。第1 行是最少变换次数。从第2 行开始，依次输出变换的图形序列。问题无解时输出“No solution!”