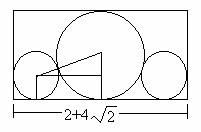
给定 n个大小不等的圆c₁ , c₂ , ……, c_n ，现要将这 n个圆排进一个矩形框中，且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。例如，当n=3，且所给的3 个圆的半径分别为1，1，2时，这3个圆的最小长度的圆排列如图所示。其最小长度为2 + 4*√ 2（说明：根号2） 。

解圆排列问题的一个随机化算法如下。
static void Circle_search(int []x,int n)
  {
        random_perm(x);
        boolean found=true;
        while(found){
            found=false;
            for(int i=1;i<=n;i++)
                for(int j=1;j<=n;j++)
                    if(MyMath.swap(x,i,j) reduces length){
                              MyMath.swap(x,i,j);
                              found=true;
                         }
             }
}
其中，random_perm(x)产生x 的一个随机排列。

根据上述算法框架，设计一个随机化算法，对于给定的n个圆，计算n个圆的最佳排列方案，使其长度尽可能小。

输入数据第一行有1个正整数n (1≤n≤20)。接下来的1行有n个数，表示n个圆的半径。

输出最小圆排列的长度