人的大脑里发生的一切是神奇的，甚至是不可理解的，正是这种神奇使得人具有自我意识。如果用普通硅片、电路、传感器制成的机器人也能进化，从而能有意识的行动，那么是否有一天，机器人也会变得和人一样有意识？电脑的硬件也许能像自然界人类和其他生物进化的方式进行进化这一想法，早在上世纪60年代就被提出，但如何着手是到1998年，因美籍华裔计算机科学家的一个灵感，才得以突破。这一灵感就是被称为达尔文芯片的高集成度可编程集成电路块，简称为DPGA。
最近，F大学计算机学院计算机神经学研究小组的科学家们发现，对达尔文芯片的关键逻辑元进行重组后产生一种奇特的现象。将若干关键逻辑元按照电路板平面坐标系2 维降序排列，经过电路演化，这些关键逻辑元自动按照x 坐标和y坐标方向延伸联接成一棵树。这棵树的每条边都平行于x 坐标轴或平行于y坐标轴。关键逻辑元构成这棵树的全部叶结点。这类树称为以关键逻辑元为叶结点的正交树。有趣的是，达尔文芯片自动产生的正交树的总边长是所有这种正交树中总边长最小的。例如，将5个关键逻辑元分别置于电路板xoy坐标系中(1,5)，(2,4)，(3,3)，(4,2)和(5,1)处，则达尔文芯片自动产生的一棵正交树如下图所示，它的总边长为12。

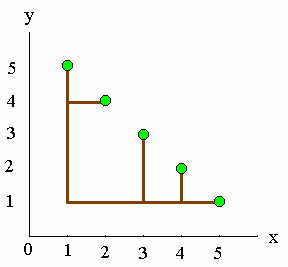
图10-3 达尔文芯片正交树

给定电路板xoy坐标系，以及电路板上n个关键逻辑元在xoy坐标系中按照2 维降序排列的位置( x_1， y₁ ) ，(x_2， y₂   ) ，……，(x_n， y_n )。其中，1<=n<=3000；0<=x₁<=x₂<=……<=x_n<= 20000；0<=y₁<=y₂<=……<=y_n<= 20000。
计算以n个关键逻辑元为叶结点的正交树中，总边长最小的最优正交树。

输入数据第1行中的整数为关键逻辑元个数n；接下来的n行中每行一个整数，依次为x₁ , x ₂, ……, x_n；最后的 n行中每行一个整数，依次为  y₁ , y₂ ,…… , y_n。

将所找到的最优正交树总边长的值，精确到小数点后2 位。