3156 停“车”问题
题目描述
国际象棋的中的棋子──车,它可以向东南西北四个方向驰骋,也是威力强大的一个棋子。但现在我们要讨论的“车”略有不同,它只能在东西或南北方向上行动。我们要在一个N╳M的矩形棋盘上安置若干辆“车”,每个格子只能放一辆“车”,在停放这些“车”时,我们可以指定每一辆“车”的停放方向,它们可以选择东西方向,使它只能威胁到在它东西方向上的格子;或者选择南北方向,只能威胁到在它南北方向上的格子。有R个格子是已经预留了车位,我们一定要把“车”放在上面;除了放在预留格的“车”外,还有C个“车”必须放进棋盘。请选择一种放置方案使没受到“车”威胁到的格子总数最多,并输出没受威胁的格子总数。
输入格式:
输入第一行由4个整数组成。分别是N(l≤N≤100), M(1≤R≤100) ,R(l≤R≤20),C(1≤C≤20)。下面是R个预留格子的坐标 ,每个坐标由两个整数X,Y(1≤X≤N,1≤Y≤M)组成,占一行。
输出格式:
输出为1行,输出没受威胁的格子总数即可。不要有多余的空格。
例如: 输入 输出
3 3 2 3 4
1 2
2 1
上述答案可用下图表示:(横杆表示东西方向的车,竖杆表示南北方向的车)
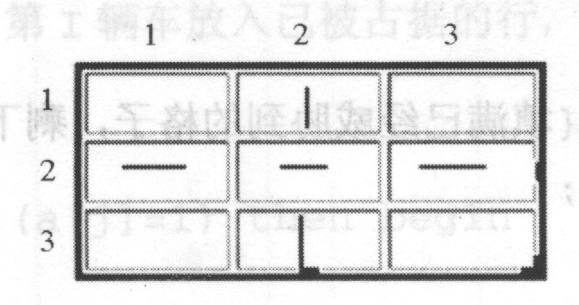
6 8 7 20 1 1 2 3 3 3 4 4 5 1 6 6 7 1
20
说明
首先要选择前R辆固定坐标的“车”的摆放方式。由于R≤20,所以最多有220种摆放可能性,又因为它们要尽量威胁到尽量少的格子,所以可以加上下面的剪枝条件:假如某一行有K(K>1)辆“车”,如果其中一辆横放,那么这一行的其他“车”也要横放(竖放同理)。
当前R辆“车”摆放方式确定后,剩下的C辆“车”可用数学方法解决它们的摆放问题。首先,把前R辆“车”威胁到的格子填满,然后剩下P辆“车”(如果有剩的话),这时删去被车占据的行和列,剩下
X╳Y的格子.假设在这些格子中因为放“车”会占据A行,B列,那这些量必须符合下面的方程:
A╳Y+B╳X-A╳B≥P A∈[0,X],B∈[0,Y] (1)
而 max{X╳Y-A╳Y-B╳X+A╳B A,B∈(1) } 则是最优解。
最后把所有最优解进行比较可求得答案。